Implementation of a Plate Cleaning Robot using ABB IRB 120

A Comprehensive Approach to Dishwashing Automation

Abstract

This project presents a comprehensive implementation of a plate cleaning robot utilizing the ABB IRB 120 robotic arm. The robot mimics human dishwashing motions through a sophisticated spiral trajectory, ensuring thorough cleaning of plates placed randomly within a predefined workspace. The system leverages numerical inverse kinematics (IK) and Proportional-Derivative (PD) control strategies for precise end-effector positioning and trajectory following. Detailed explanations of the task space definition, plate position generation, trajectory planning, and control methodologies are provided, highlighting the complexity and intricacies involved in developing such a robotic system.

Index Terms: robotics, inverse kinematics, PD control, trajectory planning, automation

I. Introduction

The automation of routine tasks, such as dishwashing, has seen significant advancements with the integration of robotic systems. This report delves into the meticulous implementation of a robotic system designed to mimic human dishwashing motions. The ABB IRB 120 robotic arm is employed in this project to perform dishwashing tasks by executing a spiral motion to clean plates, emulating human-like washing techniques. This report provides detailed explanations of the system’s components, including task space definition, inverse kinematics, control strategies, and trajectory planning.

II. System Overview

The robotic system comprises an ABB IRB 120 robotic arm programmed to navigate a defined workspace, identify plate positions, and perform cleaning operations. The core components of the system include the inverse kinematics method, task space boundaries, plate position generation, and control strategies.

A. System Flowchart

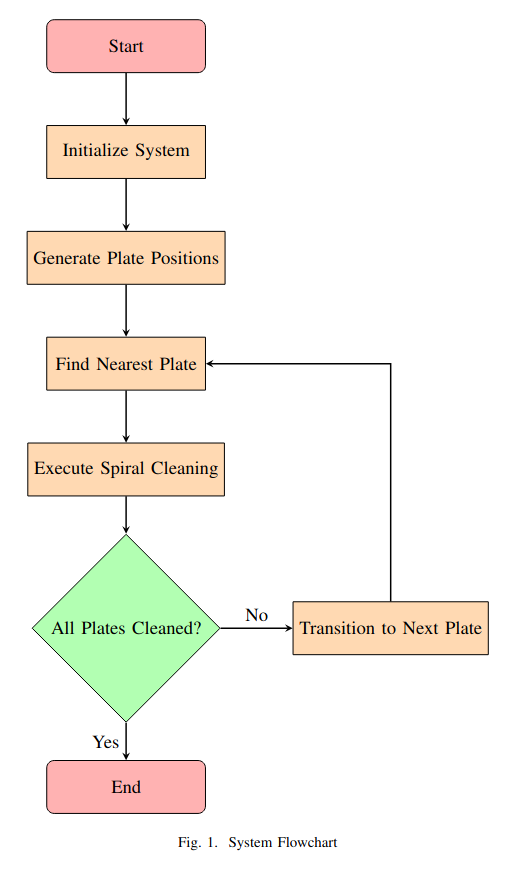
System Flowchart
Fig. 1. System Flowchart

B. Inverse Kinematics Method

Inverse kinematics (IK) is pivotal in determining the required joint angles for the robotic arm to achieve a specific end-effector position and orientation. The numerical IK method is chosen for its robustness in handling the complex configurations of the robotic arm. The IK problem is formulated as: 

Find q such that T(q) = Td

where q is the vector of joint angles, T(q) is the transformation matrix representing the end-effector pose, and Td is the desired end-effector pose.

C. Task Space Definition

The task space is defined to exclude the robot’s base area, ensuring safe operation. The boundaries are set as follows:

D. Plate Position Generation

A function is employed to generate random plate positions within the task space. The generated positions must ensure no overlap between plates and maintain a minimum distance from the robot’s base. This is achieved through the following steps:

  1. Random Position Generation: A new position Pnew is generated within the task space boundaries.
  2. Distance Calculation: The Euclidean distances between Pnew and existing plate positions Pi are calculated.
  3. Validation: The new position is validated if the distances satisfy the minimum distance constraint (minDistance = 0.28 m) and the distance from the base (baseRadius = 0.25 m).

III. Control and Motion Planning

The robot’s motion planning involves two primary phases: cleaning the plates using a spiral trajectory and transitioning between plates.

A. Spiral Trajectory for Cleaning

  1. Parameters Definition:
    • Number of points (npoints): 55
    • Radius (r): 0.145 m
    • Number of turns (nturns): 3
    • Height above plate (zabove plate): 0.05 m
  2. Trajectory Equations: 
    
θ = linspace(0, 2π · nturns, npoints)
ri = linspace(0, r, npoints)
xi = ri cos(θi) + xplate
yi = ri sin(θi) + yplate
zi = zplate + zabove plate

B. Transition Trajectory

Transitioning between plates requires generating smooth trajectories that avoid collisions with the robot’s base and other obstacles. This is achieved using a cubic polynomial trajectory planning method, which ensures smooth acceleration and deceleration phases.

  1. Waypoints Definition: Define intermediate waypoints that guide the robot around the base, avoiding obstacles.
  2. Midpoint Angle Calculation: Calculate angles for the waypoints using the atan2 function.
  3. Shortest Arc Calculation: Determine the shortest arc between angles.
  4. Midpoint Waypoints: Create intermediate waypoints along the arc at a safe distance from the base.
  5. Trajectory Planning: Use a cubic polynomial method (e.g., cubicpolytraj in MATLAB) to generate the trajectory.

IV. Trajectory Generation

A. Cleaning Trajectory

The spiral trajectory for cleaning is generated using a parametric approach, where the radius increases linearly with the angle to form a spiral: 


xi = ri cos(θi) + xplate
yi = ri sin(θi) + yplate
zi = zplate + zabove plate

B. Transition Trajectory

The transition trajectory ensures smooth movement from one plate to another. It is defined by planning the robot’s motion between intermediate waypoints: 


p(t) = a3 t³ + a2 t² + a1 t + a0

where p(t) is the position at time t and the coefficients are determined by the initial and final conditions.

V. Experimental Setup and Results

A. Initial Setup

The robot starts at the origin with a zero joint configuration. Plates are placed randomly within the task space, ensuring spacing constraints.

B. Simulation Execution

The simulation proceeds with the robot identifying the nearest unvisited plate, executing the spiral cleaning motion, and transitioning to the next plate. This loop continues until all plates are cleaned.

C. Shortest Path Calculation


dist(i) = √((xcurrent - xi)² + (ycurrent - yi)²)

The plate with the minimum distance is chosen as the next target.

D. Visualization

The simulation provides real-time visualization of the robot’s movements, including spiral and transition trajectories.

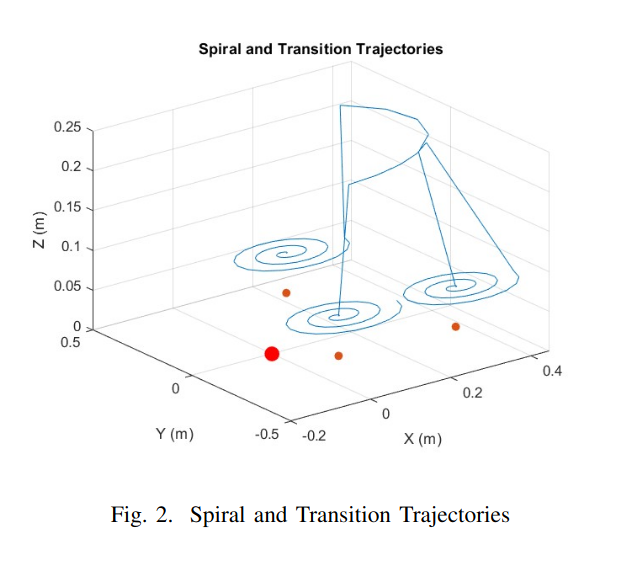
Spiral and Transition Trajectories
Fig. 2. Spiral and Transition Trajectories
Spiral Cleaning Trajectory
Fig. 3. Robot executing the spiral cleaning trajectory on plates
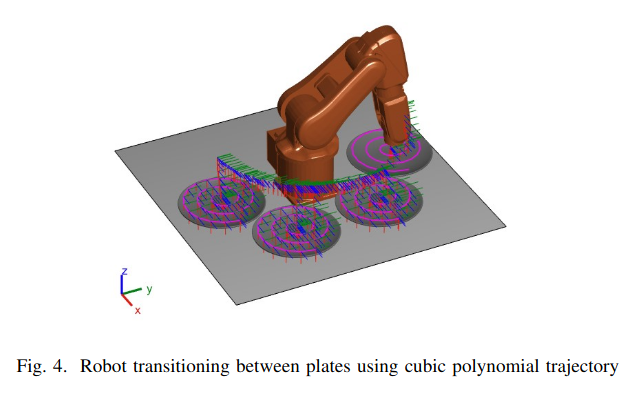
Transition Trajectory
Fig. 4. Robot transitioning between plates using cubic polynomial trajectory

VI. Conclusion

The robotic system successfully demonstrates dishwashing tasks through a controlled spiral motion. The implementation highlights the effectiveness of numerical IK methods and PD controllers in achieving precise and efficient robotic operations. Future work may include optimizing control parameters and exploring advanced trajectory planning algorithms.

MATLAB Code